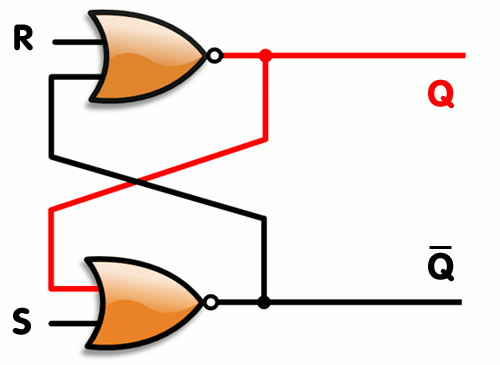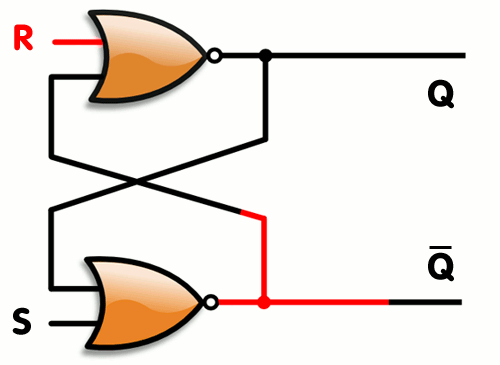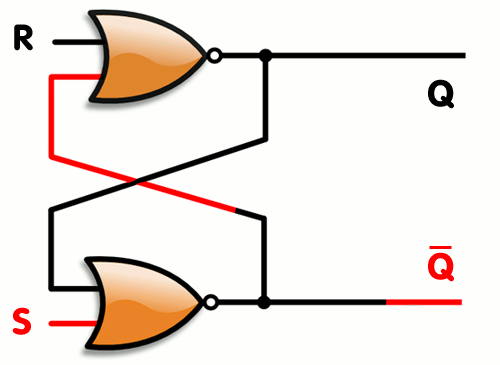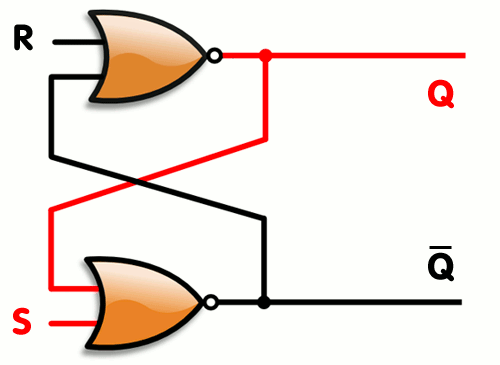
I.THIẾT KẾ BIỂU THỨC LOGIC
1.1.CÁC PHÉP TOÁN Ở ĐẠI SỐ BOOLE
Bởi vì các đại lượng chỉ có hai trạng thái nên đại số Boole rất khác đại số thường và dễ tính toán hơn. Ở đại số Boole không có phân số, số thập phân, số ảo, số phức, căn số… mà chỉ thực hiện chủ yếu 3 phép tính toán cơ bản sau:
- Phép OR
- Phép AND
- Phép phủ định NOT
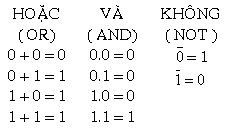
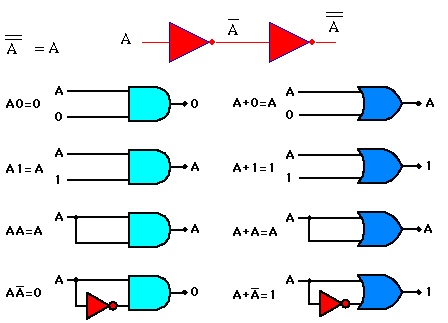
Các phép tính trên khi áp dụng cho logic 0 và 1:
1.1.1.THIẾT LẬP BIỂU THỨC LOGIC
Lập hàm logic cho từng cổng ta đã biết cho bất cứ kết nối nào của các cổng.
Từ biểu thức biết được ta có thể tính logic ra tương ứng với mỗt tổ hợp logic vào, và lập bảng sự thật của các ngõ vào (biến số) và ngõ ra (hàm).
Để tính logic ra tương ứng với một tổ hợp logic và ta thường là tính thẳng trên mạch.
Ví dụ:
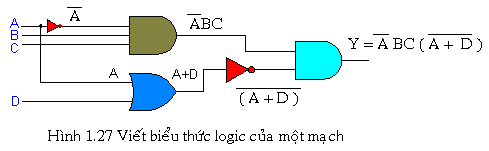
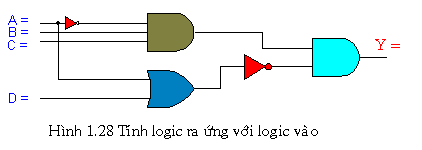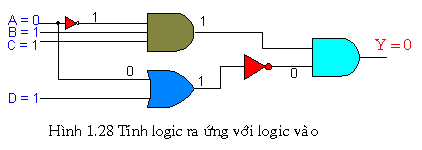
Ví dụ với mạch trên với 4 ngõ vào nên ta có tổng cộng 16 tổ hợp vào nên ta phải tính 16 trạng thái ra khác nhau mới lập được bảng sự thật (Truth Table).
1.1.2.THỰC HIỆN MẠCH TỪ BIỂU THỨC LOGIC
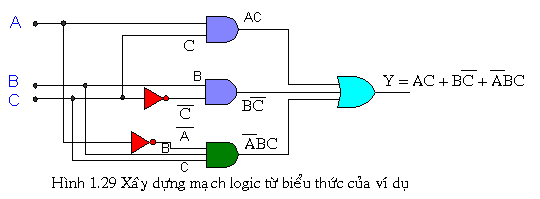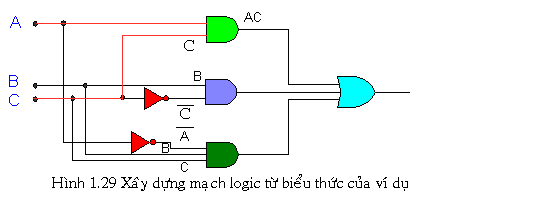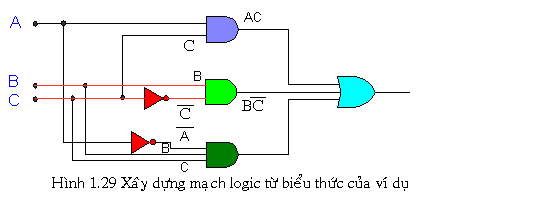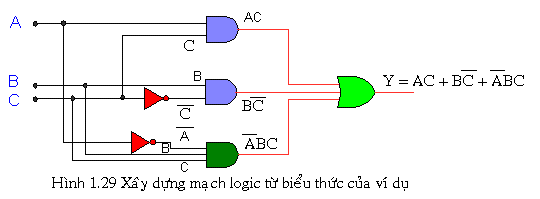
Ngược lại với viết biểu thức từ mạch là thực hiện mạch từ biểu thức logic. Ví dụ cho biểu thức logic cho là:![]() Nhìn vào biểu thức ta thấy ngõ ra là OR của 3 số hạng nên ta thực hiện mỗi số hạng Y trước. Với số hạng đầu ta dùng AND, số hạng thứ 2 ta ĐẢO C sau đó AND với B, số hạng thứ 3 ta cũng thực hiện tương tự , sau cùng ta OR 3 ba số hạng lại.
Nhìn vào biểu thức ta thấy ngõ ra là OR của 3 số hạng nên ta thực hiện mỗi số hạng Y trước. Với số hạng đầu ta dùng AND, số hạng thứ 2 ta ĐẢO C sau đó AND với B, số hạng thứ 3 ta cũng thực hiện tương tự , sau cùng ta OR 3 ba số hạng lại.
 1.2.CÁC ĐỊNH LÝ ĐẠI SỐ BOOLE
1.2.CÁC ĐỊNH LÝ ĐẠI SỐ BOOLE
- Một biến số
- Giao hoán
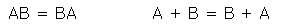
- Phối hợp
![]()
- Phân phối
![]()
- Một số đẳng thức hữu dụng
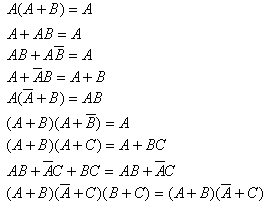
- Định lý De Morgan
![]()
Các định lý của đại số Boole được chứng minh hay kiểm chứng bằng nhiều cách. Các cách chứng minh hay kiểm chứng này tương đối đơn giản, người đọc có thể tự chứng minh hay kiểm chứng.
Ví dụ 1: Thiết kế mạch dùng hai cổng logic thỏa bảng sự thật sau đây
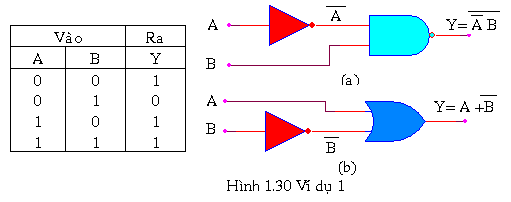
Giải:
Vì ngõ ra bằng 0 chỉ một trường hợp nên ta viết hệ thức logic ở trường hợp này. Y= 0 khi A= 0 VÀ B = 1 nên ![]() Để có Y ta đảo, nên
Để có Y ta đảo, nên![]() Mạch thực hiện cổng NOT để tạo ra A đảo, tiếp theo là cổng NAND của Avà B (hình 1.30a)
Mạch thực hiện cổng NOT để tạo ra A đảo, tiếp theo là cổng NAND của Avà B (hình 1.30a)
Mặt khác ta có thể dựa vào bảng sự thật dể viết hàm logic cho Y và kết quả là:![]()
sử dụng các định lý của đại số Boole ta biến đổi và được kết quả cuối cùng là(hình 1.30b).
![]()
Ví dụ 2: Chứng tỏ.![]()
Giải:
![]()
Vận dụng các công thức ta dể dang biến đổi được:
![]()
Một cách chứng minh khác là ta có thể dùng bảng sự thật để chứng minh biểu thức trên.
II.SỰ CHUYỂN ĐỔI GIỮA CÁC LOẠI CỔNG LOGIC
Các cổng logic có thể chuyển dổi qua lại lẫn nhau từ cổng này thành cổng khác.
Để thuận tiện cho việc thiết kế mạch logic nên phải chuyển đổi giữa các cổng với nhau, chủ yếu là chuyển đổi AND thành OR và ngược lại, chuyển đổi AND – OR thành NAND – NAND.
Đa số các bài toán thiết kế logic đều yêu cầu sử dụng cổng NAND(việc chế tạo cổng NAND đơn giản hơn các cổng khác).
Để thuận lợi cho việc chuyển đổi cần phải nắm vững các định lý của đại số Boole và đặc biệt là định lý De Morgan.
Sau đây là một số chuyển đổi giữa các cổng với nhau:
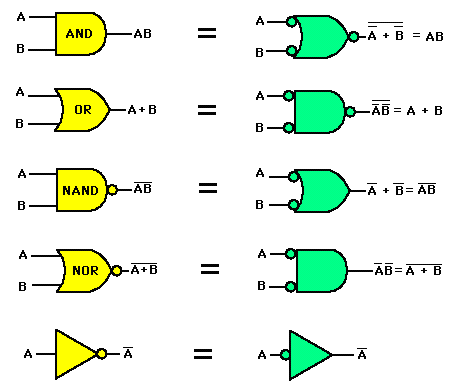
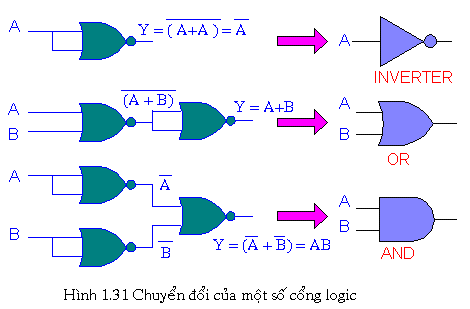 III.ÁP DỤNG CÁC ĐỊNH LÝ ĐẠI SỐ BOOLE ĐỂ RÚT GỌN BIỂU THỨC LOGIC
III.ÁP DỤNG CÁC ĐỊNH LÝ ĐẠI SỐ BOOLE ĐỂ RÚT GỌN BIỂU THỨC LOGIC
Các định lý Boole giúp đơn giản các biểu thức logic.
Việc đơn giản là cần thiết để mạch thiết kế thực hiện đơn giản và kinh tế hơn.
Rút gọn biểu thức là vận dụng các định lý từ hàm một biến cho đến hàm nhiều biến và những đẳng thức hữu dụng.
Đặt biệt là hai định lý De Morgan giúp ích cho rất nhiều trong việc rút gọn biểu thức logic và cũng là công cụ chính để chuyển đổi các dạng mạch.
Để việc rút gọn biểu thức logic và chuyển đổi mạch dể dàng cần phải nắm vững các định lý của đại số Boole và phải thông thạo chuyển đổi giữa các cổng logic.
Ví dụ 3: Rút gọn các biểu thức sau:
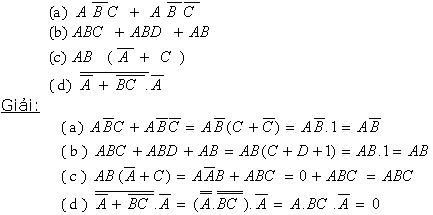
Ví dụ 4: Đơn giản hàm
![]()
Giải:
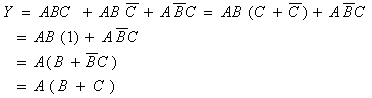
Ngoài việc rút gọn biểu thức logic bằng đại số boole, còn sử dụng đại số boole để đơn giản mạch logic. Để đơn giản mạch logic ta làm các bước sau:
– Từ mạch logic xác định biểu thức cho ngõ ra của mạch
– Sau khi xác định được hàm ngõ ra, tiến hành rút gọn biểu thức bằng cách dùng các định lý của đại số boole, đặc biệt là sử dụng định lý De Morgan.
– Sau khi được biểu thức mới, chúng ta có được mạch logic mới tương đương với mạch logic đã cho.
Ví dụ 5: Đơn giản mạch
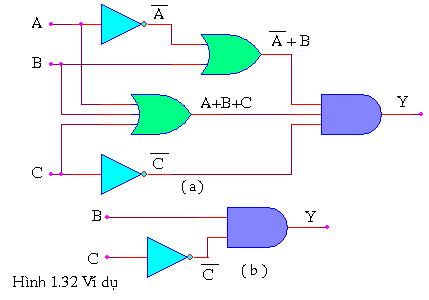
Giải:
Trước tiên ta viết biểu thức logic cho ngõ ra:
![]()
Rút gọn biểu thức ta được: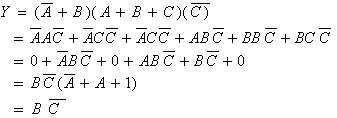
Từ biểu thức vừa rút gọn được ta thành lập được mạch logic mới như hình 1.32b.